La mayoría de los modelos de membranas publicados en la literatura son isotérmicos y, por lo tanto, no son adecuados para estudios de gestión del agua y del calor. Un número relativamente pequeño de modelos incluye efectos no isotérmicos [7, 12, 13, 15, 16] y, por lo general, los que sí se centran en modelar múltiples capas de pilas de combustible, con supuestos simplificadores para la capa de membrana. Además, muchos modelos permiten cambios de temperatura de funcionamiento, pero no un gradiente de temperatura. Para la mayoría de las condiciones, el cambio en los valores de los parámetros con la temperatura tiene un impacto más significativo que tener en cuenta los gradientes de temperatura, aunque ambos están acoplados hasta cierto punto.
Los modelos transitorios examinan cambios en los fenómenos potenciales y de transporte (caudales, producción de agua y densidad de corriente). Estos modelos tienen como objetivo examinar diferentes requisitos de carga. La mayoría de los modelos no examinan los transitorios debido al costo y la complejidad computacionales. Algunos códigos en la literatura pueden tomar del orden de decenas de minutos en determinadas circunstancias [24]. Uno de los primeros modelos en examinar transitorios en celdas de combustible PEM es un modelo a nivel de pila de Amphlett et al. [20]. Este es un modelo empírico que examina la temperatura y los caudales de gas. Ha habido algunos modelos transitorios más complejos que han examinado el comportamiento del contenido de agua en la membrana y han demostrado los efectos del secado de la membrana [10, 21]. Otros modelos transitorios no han incluido agua líquida, no informan resultados transitorios o se centran principalmente en el transporte de agua en las capas de difusión de gas [15, 16, 17, 18, 19, 20, 22]. No hay resultados reportados en la literatura que muestren simultáneamente la temperatura, el potencial, la concentración de agua y el perfil de presión en la membrana en función de las diferentes densidades de corriente, temperaturas y gradientes de presión.
El modelo presentado en este artículo es un modelo compacto que puede calcular simultáneamente la temperatura, la presión, la concentración de agua y el potencial en un número de posiciones especificado por el usuario a través de la membrana. Dado que el código utiliza funciones integradas de MATLAB, tiene solo unos pocos cientos de líneas, puede calcular cientos de puntos dentro de la membrana en segundos, se puede expandir fácilmente para incluir condiciones de contorno transitorias adicionales y se puede integrar fácilmente en un modelo general de celda de combustible. .
Los modelos de celdas de combustible de membrana de intercambio de protones (PEMFC) son necesarios para predecir el rendimiento de las celdas de combustible y optimizar el rendimiento para ayudar a reducir los costos y el tiempo de desarrollo. La gestión del agua es fundamental para las pilas de combustible eficientes debido a su gran efecto sobre los sobrepotenciales óhmicos y de transporte de masa, las condiciones de funcionamiento y el diseño del conjunto de electrodos de membrana.
Dado que la membrana es el elemento clave de una pila de combustible, se ha prestado mucha atención a ella en términos de modelado. En la literatura existen modelos tanto macroscópicos como microscópicos. Los modelos microscópicos se centran en iones individuales y efectos a nivel de poro, y los modelos macroscópicos suelen ser más empíricos y se centran en los fenómenos de transporte. Aunque los modelos microscópicos revelan información valiosa sobre lo que ocurre en la membrana, generalmente son demasiado complejos para utilizarlos en un modelo general de pila de combustible. Se supone que el sistema de membranas consta de tres componentes principales: la membrana, los protones y el agua.
La mayoría de los modelos de membrana de intercambio de polímeros son demasiado complicados. A menudo se incluyen muchos efectos secundarios, como el flujo de agua convectivo (Darcy), el hinchamiento de la membrana y otras propiedades de la membrana que dependen del contenido de agua. Son deseables modelos simples debido al tiempo reducido de desarrollo del modelo; reducir el tiempo de cálculo y facilitar la integración con otros modelos.
1.1 Revisión de la literatura
El modelado actual de pilas de combustible se centra en efectos con diseños y materiales específicos. Verbrugge y Hill [1] y Bernari y Verbrgge [2] desarrollaron un modelo unidimensional, isotérmico y de estado estacionario para el rendimiento electroquímico en una PEMFC. Afirman que la presión del líquido y del gas evoluciona por separado en la capa GDL, lo que implica que no están en equilibrio entre sí. Este modelo sólo se aplica a membranas completamente hidratadas y no se considera el flujo de arrastre debido a las moléculas de agua.
Springer, Zawodzinski y Gottesfeld [3] presentaron un modelo isotérmico unidimensional en estado estacionario de una PEMFC con énfasis en los fenómenos de transporte de agua a través de una membrana de Nafion. En [4] se desarrolló un modelo mejorado con un tratamiento detallado del transporte de iones y la conductividad iónica en el catalizador y la capa de soporte. Este modelo predijo las limitaciones del transporte masivo a altas densidades de corriente. En [5], Springer, Zawodzinski, Wilson y Gottesfeld proporcionan resultados experimentales y teóricos para efectos de estado inestable en una pila de PEMFC isotérmica 1-D. Utilizan un diagrama de frecuencia para cuantificar las influencias específicas de varias fuentes de pérdidas, como la actividad en el cátodo y la conductividad de la capa de catalizador y la membrana.
Weisbrod, Grot y Vanderborgh [6] desarrollaron un modelo a través de electrodos para predecir el rendimiento de la pila de combustible en función del equilibrio hídrico en los canales y a través de la membrana. El modelo predice la influencia tanto del espesor de la capa de catalizador como de su carga de catalizador de platino.
Nyguyen y White [7] desarrollaron un modelo unidimensional de gestión de agua y calor en estado estacionario para PEMFC. Este modelo no estudia los detalles de la membrana y las capas del catalizador por separado, ya que modela todo el electrodo como una unidad. Estabiliza el efecto de los niveles de humidificación y su efecto sobre el rendimiento de la pila de combustible. Este modelo se mejoró en [8], con la adición de un modelo lineal para la membrana y luego un modelo bidimensional en estado estacionario para el transporte de múltiples especies en los electrodos. Este modelo estudia el efecto de un distribuidor de gas interdigitado sobre el rendimiento de PEMFC. Sin embargo, no pudo predecir el efecto del agua líquida dentro del sistema. Thirumalai y White [9] utilizaron el modelo desarrollado en [8] para predecir los parámetros operativos, el diseño del campo de flujo y la geometría del colector de gas en el rendimiento de la pila de combustible.
Van Bussel, Koene y Mallant [10] crean un modelo dinámico 2D, con un modelo 1D a través de la membrana. El modelo se basa en el trabajo de Springer et al. [3], pero utiliza datos experimentales de Hinatsu, Mizhuta y Takenaka [11]. El modelo mostró que la densidad de corriente puede variar mucho a lo largo de los canales de gas, especialmente cuando se opera con gases secos.
Gurau, Kakac y Lui [12] desarrollaron un modelo 2D no isotérmico. Consideraron que el canal de gas y la capa difusora-catalizadora eran una sola entidad. El modelo muestra una distribución no uniforme de reactivos que tiene un impacto importante en la distribución de densidad de corriente. Este modelo se basa en una capa de catalizador infinitamente delgada, que es incapaz de predecir el voltaje debido a limitaciones de transporte en la capa de catalizador.
Fuller y Newmann [13] y Weber y Newmann [14] desarrollaron un modelo bidimensional en estado estacionario para el ensamblaje del electrodo de membrana. A diferencia de otros modelos, se utilizó la teoría de la solución de concentración. Argumentaron que el agua se producía en fase gaseosa en las superficies del catalizador. Su modelo es válido si no hay condensación dentro de la capa de catalizador.
El resto de este artículo está organizado de la siguiente manera: En la Sección 2, el modelo propuesto se deriva de los parámetros básicos de la celda. La Sección 3 detalla la implementación numérica del modelo, mientras que la Sección 4 presenta los resultados y las discusiones asociadas. Las conclusiones se extraen en la Sección 5.
2.0 El modelo propuesto
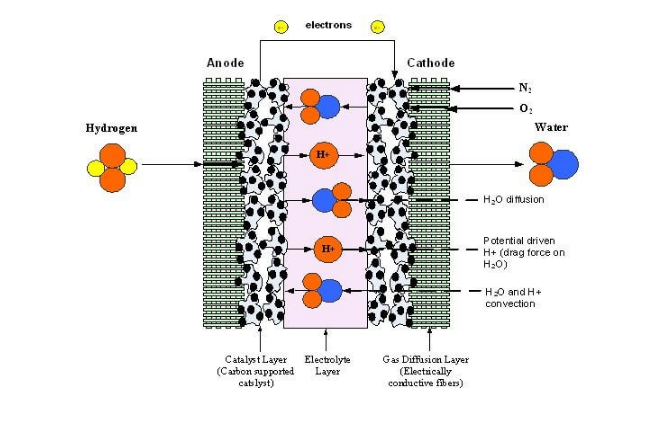
La Figura 1 muestra una membrana con flujo de agua y protones en la región 0 < y < N. Como en todos los artículos anteriores sobre fenómenos de transporte en la membrana, los protones de hidrógeno son constantes. Se requieren ecuaciones de conservación para el agua, los protones, la energía y el potencial.