La validación del modelo es el paso más importante en el proceso de construcción del modelo; sin embargo, a menudo se descuida. Incluso cuando se valida el modelo, a menudo no se hace de forma adecuada. A menudo consiste en tomar algunos puntos de datos experimentales y representarlos en el mismo gráfico que el modelo. Hay dos tipos diferentes de modelos: modelos científicos o de ingeniería y modelos estadísticos. Los modelos científicos y de ingeniería a menudo se construyen utilizando ecuaciones de la literatura y de ecuaciones derivadas. En este tipo de modelo, suele haber una combinación de ecuaciones que se utilizan para calcular los fenómenos naturales que están ocurriendo y, a menudo, hay pocos o ningún dato disponible para ayudar a construir el modelo.
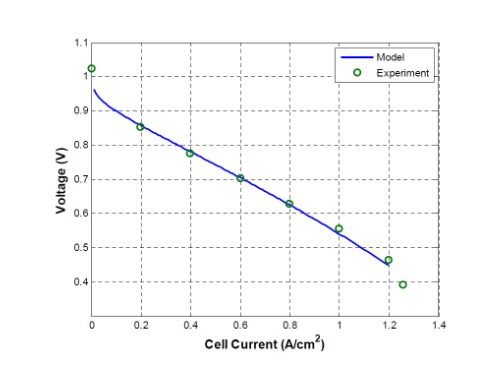
Figura 1. Comparación entre el modelo de ingeniería de pilas de combustible y los experimentos a 298 K y 1 bar.
Figura 2. Gráficos de valores previstos, reales y residuales estandarizados. (http://docs.statwing.com/interpreting-residual-plots-to-improve-your-regression/#the_top)
Figura 3. Ejemplo de buena parcela residual. (http://docs.statwing.com/interpreting-residual-plots-to-improve-your-regression/)
Si las parcelas no están distribuidas uniformemente verticalmente, tienen un valor atípico o tienen una forma. Si puede detectar un patrón o tendencia claro en sus residuos, entonces su modelo tiene margen de mejora. La mayoría de las veces, un modelo decente es mejor que ninguno. Así que tome su modelo, intente mejorarlo y luego decida si la precisión es lo suficientemente buena como para ser útil para sus propósitos.
Figura 4. Ejemplos de malas parcelas residuales. (http://docs.statwing.com/interpreting-residual-plots-to-improve-your-regression/)
Derivas en el proceso de medición
Las desviaciones en el proceso de medición se pueden verificar creando un gráfico de «orden de ejecución» o «secuencia de ejecución» de los residuos. Se trata de diagramas de dispersión en los que se traza cada residuo frente a un índice que indica el orden (en el tiempo) en el que se recopilaron los datos. Esto es útil cuando los datos se han recopilado en un orden de ejecución aleatorio, o en un orden que no aumenta ni disminuye en ninguna de las variables predictivas. Si los datos aumentan o disminuyen con las variables predictivas, entonces la deriva en el proceso puede no separarse de la relación funcional entre los predictores y la respuesta; es por eso que se fomenta la aleatorización al planificar el diseño de experimentos.
Figura 5. Ejemplo de gráfico de orden de ejecución.
Errores aleatorios independientes
Un gráfico de retardos de residuos ayuda a evaluar si los errores aleatorios son independientes entre sí. Si los errores son independientes, la estimación del error en la desviación estándar estará sesgada, lo que lleva a inferencias inadecuadas sobre el proceso. El gráfico de retraso funciona trazando cada valor residual versus el valor del residual sucesivo. Debido a la forma en que se emparejan los residuos, habrá un punto menos que la mayoría de los otros tipos de gráficos de residuos.
No habrá ningún patrón o estructura en el gráfico de retraso si los errores son independientes. Los puntos aparecerán dispersos aleatoriamente a lo largo de la gráfica, y si hay una dependencia significativa entre los errores, habrá algún tipo de patrón determinista que sea evidente.
Figura 6. Ejemplo de gráfico de retraso.
Problemas potenciales del modelo
Figura 7. Problemas potenciales del modelo expuestos por los residuos.
Figura 8. Varianza no constante de los términos de error.
Términos del modelo faltantes
Los gráficos de residuos son la herramienta más valiosa para evaluar si faltan variables en la parte funcional del modelo. Sin embargo, si los resultados son confusos, puede resultar útil utilizar pruebas estadísticas para la hipótesis del modelo. Uno podría preguntarse si podría ser más útil pasar directamente a las pruebas estadísticas (ya que son más cuantitativas); sin embargo, los gráficos residuales proporcionan la mejor información general sobre el ajuste del modelo. Estas pruebas cuantitativas se denominan pruebas de “falta de ajuste” y hay muchas de ellas en cualquier libro de texto de estadística.
La estrategia más comúnmente utilizada es comparar la cantidad de variación de los residuos con una estimación de la variación aleatoria del modelo utilizando un conjunto de datos adicional. Si la variación aleatoria es similar, entonces se puede suponer que no faltan términos en el modelo. Si la variación aleatoria del modelo es mayor que la variación aleatoria del conjunto de datos independiente, entonces es posible que falten términos o que no estén especificados en la parte funcional del modelo.
Comparar la variación entre los conjuntos de datos experimentales y del modelo es muy útil; sin embargo, hay muchos casos en los que no se dispone de una medición replicada. Si este es el caso, entonces las estadísticas de falta de ajuste se pueden calcular dividiendo la desviación estándar residual en dos estimadores independientes de la variación aleatoria en el proceso.
Un estimador depende del modelo y las medias de los conjuntos de datos replicados (σm), y el otro estimador es una desviación estándar de la variación observada en cada conjunto de mediciones replicadas (σr). Los cuadrados de estos dos estimadores a menudo se denominan “cuadrados medios por falta de ajuste”. El estimador del modelo se puede calcular mediante [10]:
donde p es el número de parámetros desconocidos en el modelo, n es el tamaño de muestra del conjunto de datos utilizado para ajustar el modelo, nu es el número de combinaciones de niveles de variables predictivas, es el número de observaciones replicadas en la iésima combinación de predictores niveles variables.
Si el modelo se ajusta bien, el valor de la función sería una buena estimación del valor medio de la respuesta para cada combinación de valores de variables predictivas. Si la función proporciona buenas estimaciones de la respuesta media en la i-ésima combinación, entonces σm debería tener un valor cercano a σr y también debería ser una buena estimación de σ. Si al modelo le faltan términos importantes, o alguno de los términos está especificado correctamente, entonces la función proporcionará una estimación deficiente de la respuesta media para alguna combinación de predictores, y σm probablemente será mayor que σr.
El estimador dependiente del modelo se puede calcular usando [10]:
Dado que σr depende sólo de los datos y no de la parte funcional del modelo, esto indica que σr será un buen estimador de σ, independientemente de si el modelo es una descripción completa del proceso. Normalmente, si σm > σr, entonces una o más partes del modelo pueden faltar o estar especificadas incorrectamente. Debido al error aleatorio en el modelo, a veces σm será mayor que σr incluso cuando el modelo sea preciso. Para asegurar que la hipótesis del modelo no sea rechazada por accidente, es necesario comprender cuánto mayor puede ser σr posible. Esto asegurará que la hipótesis sólo se rechace cuando σm sea mayor que σr. Una relación que se puede utilizar cuando el modelo se ajusta a los datos es [10]:
La probabilidad de rechazar la hipótesis está controlada por la distribución de probabilidad que describe el comportamiento del estadístico, L. Un método para definir el valor de corte es usar el valor de L cuando es mayor que el valor de corte de la cola superior de la Distribución F. Esto permite un método cuantitativo para determinar cuándo σm es mayor que σr.
La probabilidad especificada por el valor límite de la distribución F se denomina «nivel de significancia» de la prueba. El valor de significancia más comúnmente utilizado es α = .05, lo que significa que la hipótesis de un modelo adecuado sólo será rechazada en el 5% de las pruebas para las que el modelo realmente es adecuado. Los valores de corte se pueden calcular utilizando la distribución F descrita en la mayoría de los libros de texto de estadística.
Términos innecesarios en el modelo
A veces los modelos se ajustan muy bien a los datos, pero hay términos adicionales innecesarios. Se dice que estos modelos “se ajustan demasiado” a los datos. Dado que los parámetros de cualquier término innecesario en el modelo suelen tener valores cercanos a cero, puede parecer inofensivo dejarlos en el modelo. Sin embargo, si hay muchos términos adicionales en el modelo, podría haber casos en los que el error del modelo sea mayor de lo necesario y pueda afectar las conclusiones extraídas de los datos.
El sobreajuste ocurre a menudo cuando se desarrollan modelos puramente empíricos para datos experimentales, con poca comprensión de la variación total y aleatoria de los datos. Esto sucede cuando los métodos de regresión se ajustan al conjunto de datos en lugar de utilizar funciones para describir la estructura de los datos. Hay modelos que a veces se fabrican para adaptarse a patrones muy complejos, que en realidad pueden ser una estructura final en el ruido si el modelo se analiza cuidadosamente.
Para determinar si un modelo tiene demasiados términos, también se pueden utilizar pruebas estadísticas. Las pruebas de sobreajuste de los datos son un área en la que las pruebas estadísticas son más efectivas que los gráficos residuales. En este caso, se utilizan pruebas individuales para cada parámetro del modelo en lugar de una prueba única. Las estadísticas de prueba para comprobar si cada parámetro es cero o no normalmente se basan en la distribución T. Cada estimación de parámetro en el modelo se mide en términos de cuántas desviaciones estándar tiene de su valor hipotético de cero. Si el valor estimado del parámetro está lo suficientemente cerca de los valores hipotéticos como para que cualquier desviación adicional pueda atribuirse a un error aleatorio, entonces se acepta la hipótesis de que el valor verdadero del parámetro no es cero. Sin embargo, si el valor estimado del parámetro está tan alejado del valor hipotético que la desviación no puede explicarse de manera plausible mediante un error aleatorio, se rechaza la hipótesis de que el valor verdadero del parámetro es cero.
El estadístico de prueba para cada una de estas pruebas es simplemente el valor estimado del parámetro dividido por su desviación estándar estimada:

 que denota la iésima respuesta en el conjunto de datos y
que denota la iésima respuesta en el conjunto de datos y representa la lista de variables explicativas, cada una establecida en los valores correspondientes encontrados en la iésima observación del conjunto de datos. La distancia desde la línea en 0 es qué tan mala es la predicción para ese valor. Dado que el Residual = Observado – Predicho, los valores positivos para el residual (en el eje y) significan que la predicción fue demasiado baja, y los valores negativos significan que la predicción fue demasiado alta; 0 significa que la suposición fue exactamente correcta.
representa la lista de variables explicativas, cada una establecida en los valores correspondientes encontrados en la iésima observación del conjunto de datos. La distancia desde la línea en 0 es qué tan mala es la predicción para ese valor. Dado que el Residual = Observado – Predicho, los valores positivos para el residual (en el eje y) significan que la predicción fue demasiado baja, y los valores negativos significan que la predicción fue demasiado alta; 0 significa que la suposición fue exactamente correcta.











